METODE GRAFIK
Setelah dapat membuat Model Matematika (merumuskan) persoalan Program Linier, maka untuk menentukan penyelesaian Persoalan Program Linier dapat menggunakan 2 metode, yaitu: Metode Grafik dan Metode Simpleks.
Catatan : Metode Grafik hanya dapat digunakan dalam pemecahan masalah program linier yang ber “dimensi” : 2 x n atau m x 2, karena keterbatasan kemampuan suatu grafik dalam “menyampaikan” sesuatu (sebenarnya grafik 3 dimensi dapat digambarkan, tetapi sangat tidak praktis).
FUNGSI TUJUAN MAKSIMISASI
A. FORMULASI PERMASALAHAN
Metode grafik hanya bisa digunakan untuk menyelesaikan permasalahan dimana hanya terdapat dua variabel keputusan. Untuk menyelesaikan permasalahan tersebut, langkah pertama yang harus dilakukan adalah memformulasikan permasalahan yang ada ke dalam bentuk Linear Programming (LP). Langkah-langkah dalam formulasi permasalahan adalah :
1. Indentifikasi variabel keputusan
2. Indentifikasi fungsi obyektif
3. Identifikasi kendala-kendala
4. Menggambarkan bentuk grafik dari semua kendala
5. Indentifikasi daerah solusi yang layak pada grafik
6. Menggambarkan bentuk grafik dari fungsi obyektif dan menentukan titik yang memberikan nilai obyektif optimal pada daerah solusi yang layak.
7. Mengartikan solusi yang diperoleh
Contoh Soal :
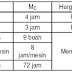
“PT. Rakyat Bersatu” menghasilkan 2 macam produk. Baik produk I maupun produk II setiap unit laku Rp. 3000,-. Kedua produk tersebut dalam proses pembuatannya perlu 3 mesin. Produk I perlu 2 jam mesin A, 2 jam mesin B, dan 4 jam mesin C. Produk II perlu 1 jam mesin A, 3 jam mesin B, dan 3 jam mesin C. Tersedia 3 mesin A yang mampu beroperasi 10 jam per mesin per hari, tersedia 6 mesin B yang mampu beroperasi 10 jam per mesin per hari, dan tersedia 9 mesin C yang mampu beroperasi 8 jam per mesin per hari. Berikan saran kepada pimpinan “PT. Rakyat Bersatu” sehingga dapat diperoleh hasil penjualan yang maksimum ! Dan berapa unit produk I dan produk II harus diproduksi ?
Jawab:
1. Langkah Pertama (Identifikasi Variabel Keputusan)
Misalkan: produk I = X1
produk II =X2
2. Langkah Kedua (Identifikasi Fungsi Obyektif/Tujuan)
Max Z = 3000 X1 + 3000 X2
3. Langkah Ketiga (Identifikasi Kendala-Kendala) *Lihat tabel 1.
2X1 + X2 ≤ 30 ...........i)
2X1 + 3X2 ≤ 60 ..........ii)
4X1 + 3X2 ≤ 72 .........iii)
X1 ≥ 0; X2 ≥ 0 (Syarat Non Negatif)
4. Langkah Keempat (Menggambarkan Bentuk Grafik)
a) Untuk persamaan 2X1 + X2 = 30 ….. (i)
à 2X1 + X2 = 30
X2 = 0, X1 = 15
X1 = 0, X2 = 30
\ didapat titik potong = (15 , 30)
b) Untuk persamaan 2X1 + 3X2 = 60 ....(ii)
à2X1 + 3X2 = 60
X2 = 0, X1 = 30
X1 = 0, X2 = 20
\ didapat titik potong = (30 , 20)
c) Untuk persamaaan 4X1 + 3X2 = 72 ....(iii)
à4X1 + 3X2 = 72
X2 = 0, X1 = 18
X1 = 0, X2 = 24
\didapat titik potong = (18 , 24)
*Lihat grafik 1.
5. Langkah Kelima (Identifikasi Daerah Solusi yang Layak)
Titik-titik yang layak memenuhi semua keterbatasan sumber daya tersebut berada di daerah bergaris pada Gambar grafik tersebut. Daerah yang layak ini dikelilingi oleh titik-titik pojok (titik ekstrim) 0, A, B, C, D.
6. Langkah Keenam (Menentukan Titik Yang Memberikan Nilai Obyektif Optimal Pada Daerah Solusi Yang Layak)
Jadi daerah yang memenuhi ke-5 daerah tersebut terletak di dalam daerah yang dibatasi oleh titik-titik O(0,0), A(15,0), D(0,20), titik B yaitu titik potong antara garis 2X1 + X2 = 30 dan garis 4X1 + 3X2 = 72 , dan titik C adalah titik potong antara garis 2X1 + 3X2 = 60 dan garis 4X1 + 3X2 = 72.
n Titik B perpotongan antara garis 2X1 + X2 = 30 dan garis 4X1 + 3X2 = 72, dengan mengeliminasi X1, dapat dihitung :
2X1 + X2 = 30 |*2 → 4X1 + 2X2 = 60 ........i)
4X1 + X2 = 72 |*1 → 4X1 + 3X2 = 72 ….....iii)
__________________ -
- X2 = - 12 à X2 = 12
à X1 = 9 maka titik B adalah (9,12)
n Titik C perpotongan antara garis 2X1 + 3X2 = 60 dan garis 4X1 + 3X2 = 72, dengan mengeliminasi X2, dapat dihitung :
2X1 + 3X2 = 60 ............i)
4X1 + 3X2 = 72 ............iii)
____________________ -
- 2X1 = - 12 à X1 = 6
à X2 = 16 maka titik C adalah (6,16)
Jadi titik-titik sudutnya adalah : O(0,0), A(15,0), B(9,12), C(6,16), dan D(0,20).
Penyelesaian dari soal diatas adalah menghitung nilai fungsi sasaran (Z = 3000 X1 + 3000 X2) di setiap titik sudut-titik sudut Daerah yang Memenuhi Kendala, sehingga:
n Titik O (0,0) à Z (0,0) = 3000.(0) + 3000.(0) = 0,
n Titik A (15,0) à Z (15,0) = 3000.(15) + 3000.(0) = 45.000
n Titik B (9,12) à Z (9,12) = 3000.(9) + 3000.(12) = 63.000
n Titik C (6,16) à Z(6,16) = 3000.(6) + 3000.(16) = 66.000
n Titik D (0,20) à Z(0,20) = 3000.(0) + 3000.(20) = 60.000
7. Langkah Ketujuh (Mengartikan Solusi yang diperoleh)
Fungsi Tujuan adalah mencari nilai maksimumnya sehingga nilai yang sesuai adalah :
n Terletak pada titik C(6,16)
n Dengan nilai fungsi tujuannya Rp. 66.000,00
Sehingga agar diperoleh laba yang maksimum maka Pimpinan ”PT. Rakyat Bersatu” harus memproduksi :
n Produk I sebanyak 6 unit dan
n Produk II sebanyak 16 unit
sehingga mendapat laba maksimum sebesar Rp.66.000,00
FUNGSI TUJUAN MINIMISASI
Permasalahan minimisasi dapat juga diselesaikan secara grafik. Langkah-langkah penyelesaian permasalahan sama dengan penyelesaian permasalahan untuk fungsi tujuan maksimisasi yaitu: formulasi permasalahan, menentukan area layak, serta menentukan solusi optimal. Minimisasi dapat berupa meminimumkan biaya produksi.
Contoh soal:
Perusahaan makanan ROYAL merencanakan untuk membuat dua jenis makanan yaitu Royal Bee dan Royal Jelly. Kedua jenis makanan tersebut mengandung vitamin dan protein. Royal Bee paling sedikit diproduksi 2 unit dan Royal Jelly paling sedikit diproduksi 1 unit. Tabel berikut menunjukkan jumlah vitamin dan protein dalam setiap jenis makanan:
Bagaimana menentukan kombinasi kedua jenis makanan agar meminimumkan biaya produksi.
Langkah – langkah:
1. Langkah Pertama (Menentukan Variabel)
X1 = Royal Bee
X2 = Royal Jelly
2. Langkah Kedua (Menentukan Fungsi Tujuan)
Zmin = 100X1 + 80X2
3. Syarat Ikatan (Menentukan Fungsi Kendala) :
à 2X1 + X2 ≥ 8 (vitamin)
è 2X1 + 3X2 ≥ 12 (protein)
è X1 ≥ 2 * Lihat tabel 2
è X2 ≥ 1
4. Langkah Keempat (Membuat grafik)
à2X1 + X2 = 8
X1 = 0, X2 = 8
X2 = 0, X1 = 4
à2X1 + 3X2 = 12 * Lihat grafik 2
X1 = 0, X2 = 4
X2 = 0, X1 = 6
àX1 = 2
àX2 = 1
5. Langkah Kelima (Identifikasi Daerah Solusi yang Layak)
Titik-titik yang layak memenuhi semua keterbatasan sumber daya tersebut berada di daerah bergaris pada Gambar grafik tersebut. Daerah yang layak ini dikelilingi oleh titik-titik A, B, C.
6. Langkah Keenam (Menentukan Titik Yang Memberikan Nilai Obyektif Optimal Pada Daerrah Solusi Layak)
· Titik A yaitu titik potong antara X2 = 1 dengan garis 2X1 + 3X2 = 12, untuk mencari nilai X1 dengan menggunakan metode Substitusi sebagai berikut :
2X1 + 3X2 = 12
2X1 + 3(1) = 12
2X1= 9
X1 = 4.5
TITIK A = (4.5 , 1)
· Titik B yaitu titik potong antara garis 2X1 + X2 = 8 dan garis 2X1 + 3X2 = 12, Adapun cara menghitung titik B dengan menggunakan metode Eliminasi dan Substitusi sebagai berikut:
2X1 + X2 = 8........i)
2X1 + 3X2 = 12 ….....ii)
__________________ -
-2X2 = -4 « X2 = 2
masukkan X2 ke kendala (1)
2X1 + X2 = 8
2X1 + 2 = 8
2 X1 = 6 « X1 = 3
TITIK B = (3 , 2)
· Titik C yaitu titik potong antara X1 = 2 dengan garis 2X1 + X2 = 8, untuk mencari nilai X1 dengan menggunakan metode Substitusi sebagai berikut :
2X1 + X2 = 8
2(2) + X2 = 8
X2 = 4
TITIK C = (2 , 4)
Penyelesaian dari soal diatas adalah menghitung nilai fungsi sasaran
(Z min = 100X1 + 80X2 ) , sehingga:
· Titik A (4.5 , 1) :
Z min = 100X1 + 80X2
= 100 . 4,5 + 80 . 1
= 450 + 80 = 530
· Titik B (3 , 2):
Z min = 100X1 + 80X2
= 100 . 3 + 80 . 2
= 300 + 160 = 460
· Titik C (2 , 4):
Z min = 100X1 + 80X2
= 100 . 2 + 80 . 4
= 200 + 320 = 520
7. Langkah Ketujuh (Mengartikan Solusi yang diperoleh)
Fungsi Tujuan adalah mencari nilai minimumnya sehingga nilai yang sesuai adalah :
n Terletak pada titik B (3 , 2)
n Dengan nilai fungsi tujuannya Rp. 460.000
Sehingga untuk meminimumkan biaya produksi maka Perusahaan Makanan Royal memproduksi:
n Royal Bee sebanyak 3 unit dan
n Royal Jelly sebanyak 2 unit
Dengan biaya sebesar Rp.460.000
















metode grafik ialah suatu metode yang berfungsi menyelesaikan persamaan non-linear.metode ini juga digunakan untuk mendapatkan akar perkiraan dari persamaan f(x) = 0 dengan membuat plot dari fungsi dan mengamatinya di mana fungsi tersebut memotong sumbu x. Di titik ini, yang merepresentasikan nilai x yang membuat f(x) = 0, memberikan hampiran kasar bagi akar persamaan itu. Keterbatasan metode ini adalah variabel yang bisa digunakan terbatas (hanya dua), penggunaan 3 variabel akan sangat sulit dilakukan.
BalasHapusthx bro, ngebantu bnged buad tugas saya
BalasHapus